3. 데이터베이스 구축 - 논리 데이터베이스 설계 (관계 대수와 관계 해석)
86-1. 관계 대수
: 관계형 데이터베이스에서 원하는 정보를 얻기 위한 유도 방법을 기술하는 절차적인 언어
- 관계 대수는 릴레이션을 처리하기 위한 연산자와 연산 규칙을 제공하는 언어이다.
- 폐쇄 성질 (Closure property) : 관계 대수의 피연산자는 릴레이션이며 연산 결과도 릴레이션이다.
- 절차적 언어 : 질의에 대한 해를 구하기 위해 수행해야 하는 연산의 순서를 명시한다.
- 순수 관계 연산자와 일반 집합 연산자로 나뉜다.
1) 일반 집합 연산자 (Set Operations)
: 수학의 집합 이론에서 사용되는 연산. 릴레이션 역시 튜플의 집합이므로 적용이 가능하다.
- 일반 집합 연산자 중 합집합, 교집합, 차집합의 경우 두 릴레이션이 서로 합병 가능해야 연산이 가능하다.
※ 합병 조건 (Union-compatibility)
: 두 릴레이션 R과 S의 차수가 같고 (속성의 수가 같고), 대응되는 속성별로 도메인이 같다.
- 두 릴레이션 R과 S가 서로 합병 가능이라면 R의 i번째 속성과 S의 i번쨰 속성은 도메인이 같다.
- 그러나 속성 이름도 같을 필요는 없다.
1. 합집합 (Union, ∪)
: 두 릴레이션 R과 S 내에 존재하는 튜플의 합집합
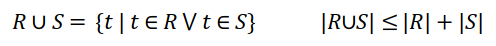
- 두 릴레이션에 속하는 모든 튜플을 중복을 제거하여 포함한다.
- 합집합 결과 릴레이션의 카디널리티는 두 릴레이션의 카디널리니티의 합 이하이다.
- 합집합 결과 릴레이션의 차수는 두 릴레이션의 차수와 같다.
2. 교집합 (Intersect, ∩)
: 두 릴레이션 R과 S 내에 존재하는 튜플의 교집합

- 두 릴레이션에 동시에 속하는 튜플을 포함한다.
- 교집합 결과 릴레이션의 카디널리티는 두 릴레이션의 카디널리티 중 최소값 이하이다.
- 교집합 결과 릴레이션의 차수는 두 릴레이션의 차수와 같다.
3. 차집합 (Difference, -)
: 두 릴레이션 R과 S 내 존재하는 튜플의 차집합

- 두 릴레이션 R과 S의 차집합 R - S는 R에는 속하지만 S에는 속하지 않는 튜플을 포함한다.
- 교집합, 합집합, 카티션 프로덕트와 달리 교환적(Commutative)이지 않고, 결합적(Associative)이지 않다. 즉,

- 릴레이션 R과 S의 차집합 결과 릴레이션 R - S의 카디널리티는 R의 카디널리티 이하이다.
- 차집합 결과 릴레이션의 차수는 두 릴레이션의 차수와 같다.
4. 카티션 프로덕트(Cartesian Product, 교차곱, ×)
: 두 릴레이션 R과 S 내에 존재하는 튜플들의 순서 쌍

- 두 릴레이션에 속한 튜플들을 접속(concatenation; ·)시킨 튜플을 포함한다.
- 카티션 프로덕트 결과 릴레이션의 카디널리티는 두 릴레이션의 카디널리티의 곱과 같다.
- 카티션 프로덕트 결과 릴레이션의 차수는 두 릴레이션의 차수의 합과 같다.

2) 순수 관계 연산자 (Relational Operations)
: 관계 데이터베이스에 적용하기 위해 특별히 개발된 연산
1. 셀렉트 (Select)
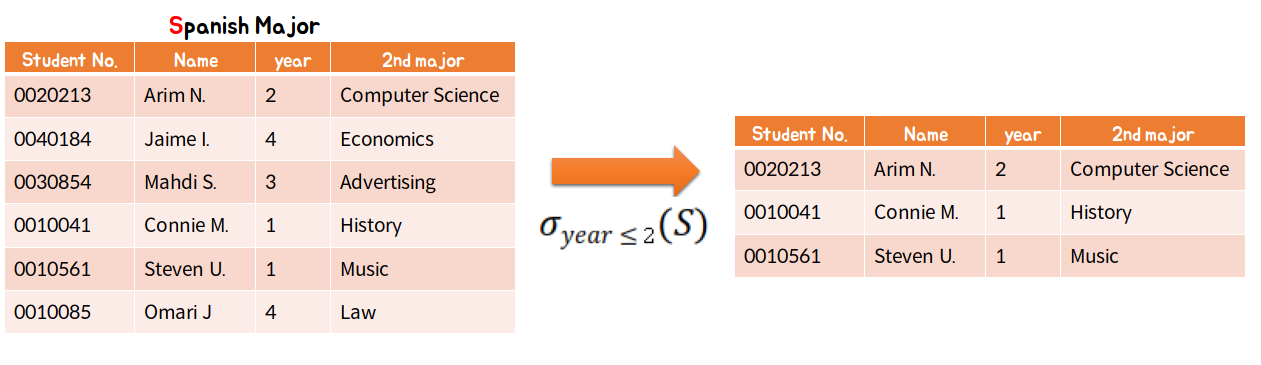
: 릴레이션 내 존재하는 튜플 중에서 선택 조건을 만족하는 튜플의 부분집합으로 이루어진 릴레이션 생성

- 릴레이션의 행(가로)에 해당하는 튜플을 구하는 수평 연산(Horizontal operation)이다.
- 비교연산자(=, !=, <, >, ≤, ≥)와 논리연산자(∧:and, ∨:or, ㄱ:not)을 이용해 조건을 표시한다.
2. 프로젝트 (Project)
: 릴레이션 내 속성 중 원하는 속성 리스트만을 추출하여 릴레이션 생성

- 릴레이션의 열(세로)에 해당하는 속성을 추출하는 수직 연산 (Vertial operation)이다.
- 연산 결과로 만들어진 릴레이션에 중복이 있다면 제거한다.

3. 조인 (Join)
: 공통 속성을 중심으로 두 릴레이션을 합쳐 새로운 릴레이션을 생성
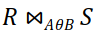
- 릴레이션 R의 속성 r과 릴레이션 S의 속성 s를 이용해 두 릴레이션을 합친다
- 조인 결과로 만들어진 릴레이션의 차수는 두 릴레이션의 차수의 합과 같다.
- 두 릴레이션 R과 S의 공통 속성 r, s를 이용한 조인은 R과 S의 카티션 프로덕트에서 r=s 조건으로 셀렉트 연산을 수행한 것과 같다. 즉,
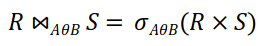
- 자연조인 (Natural join) : 조인 조건이 '=' 일 때 같은 속성이 두번 나타나게 되는데, 이때 중복되는 속성을 제거하여 한번만 나타낸 것
- 자연조인이 성립하려면 두 릴레이션의 공통 속성의 이름과 도메인이 같아야 한다.

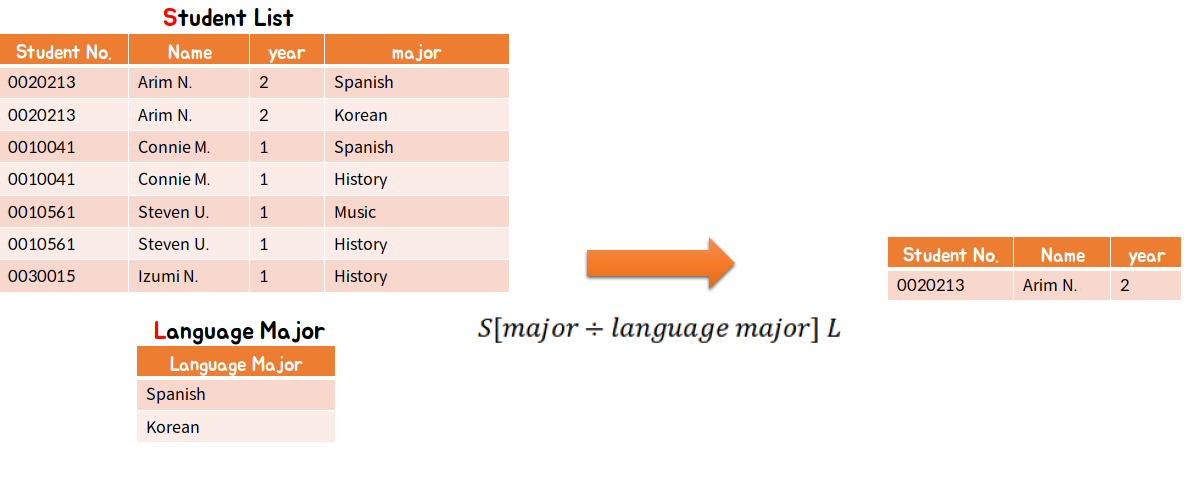
4. 디비전 (Division)
: 속성 집합 X를 가진 릴레이션 R과 속성 집합 Y를 가진 릴레이션 S에 대해 X⊃Y 일때, S(Y)의 모든 튜플에 연관된 R의 튜플을 포함하여 속성 Y를 제외하고 릴레이션으로 생성
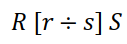
- 나누어지는 릴레이션의 차수가 (m+n), 나누는 릴레이션의 차수가 n일 때 디비전 결과 릴레이션의 차수는 m이다.
- 나누어지는 릴레이션은 나누는 릴레이션의 모든 속성을 공통으로 포함한다.
- R ÷ S의 결과 릴레이션을 S와 카티션프로덕트한 결과 릴레이션은 R의 부분집합이다. 즉,
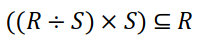
86-2. 관계 해석
: 수학의 술어 해석(Predicate Calculus)를 기반으로한 관계 데이터베이스 연산 방법
- 관계 데이터베이스를 제안한 E.F. Codd가 제안하였다.
- 비절차적 언어 : 원하는 정보가 무엇이라는 것만 선언하는 비절차적 특성을 지닌다.
- 술어(Predicate) : 실행 결과가 반드시 참(true)이거나 거짓(false)이 되는 함수
- 튜플 관계 해석과 도메인 관계 해석으로 나뉜다.
- 튜플 관계 해석 : 원하는 릴레이션을 튜플 해석식 (tuple calculus expression)으로 정의하는 표기법
- 도메인 관계 해석 : 원하는 릴레이션을 도메인 해석식 (domain calculus expression)으로 정의하는 표기법
- 튜플 관계 해석과 도메인 관계 해석은 표현 방법에는 차이가 있으나 표현 능력과 처리 기능은 동등하다.