About Data(3)
13. Similarity and Dissimilarity (유사도와 비유사도)
1. Simila rity (유사도)
- 두 데이터 객체가 얼마나 같은지에 대한 수치 측정
- 두 객체가 비슷할 수록 값이 높다
- 범위 : [0, 1]
2. Dissimilarity (비유사도)
- 두 데이터 객체가 얼마나 다른지에 대한 수치 측정
- 두 객체가 비슷할 수록 값이 낮다
- 최소 dissimilarity는 0이지만, 최댓값은 다양할 수 있음
※Proximity (근접도) : similarity와 dissimilarity를 모두 가리킴
14. Data Matrix (데이터 행렬) / Dissimilarity Matrix (차이 행렬)
1. Data Matrix

- n개의 attribute를 가진 m개의 data objects를 행렬로 저장
-> two modes (data object, attribute)
2. Dissimilarity Matrix

- n개의 data object들의 서로간 distance를 행렬로 저장
- d(i,j) == d(j,i) 이므로, triangular matrix라고 할 수 있음
- single mode (data object)

15. Proximity Measure (근접도 측정)
15-1. Proximity Measure for Nominal Attributes (명목형 속성의 근접도 측정)
- nominal attribute는 2가지 이상의 state를 가짐 ex) hair_color = {black, brown, red, yellow}
- 방법 1 : Simple Matching
- m이 일치하는 attribute의 수이고, p가 총 attribute의 수일때, data object i와 j의 dissimilarity
d(i, j) = (p - m) / p
- 방법 2 : 여러개의 binary attribute로 바꾸어 계산
- nominal attribute의 각각의 state에 대한 binary attribute를 생성하고, 근접도를 측정
- ex) hair_color attribute의 state가 {black, brown, red, yellow}으로 4가지 일때, 각 state에 대한 Y/N의 binary attrbute를 생성
15-2. Proximity Measures for Binary Attributes (이진형 속성의 근접도 측정)

- binary data에 대한 contingency table(분할표)를 계산
- q : 객체 i와 객체 j 모두 값이 1인 attribute의 수
- r : 객체 i는 1, 객체 j는 0의 값인 attribute의 수
- s : 객체 i는 0, 객체 j는 1의 값인 attribute의 수
- t : 객체 i와 객체 j 모두 값이 0인 attribute의 수
- symmetric binary variable의 경우 distance는 d(i, j) = (r + s) / (q + r + s + t)
- asymmetric binary variable의 경우 distance는 d(i, j) = (r + s) / (q + r + s) (흔한 값인 t가 분모에 있으면 d값간의 비교가 어렵기 때문)
- Jaccard coefficient (자카드 계수) : 두 집합간의 유사도 Dissimilarity (유사도와 비유사도)
- asymmetric binary variable의 Jaccard coefficient는

16. Standardizing Numeric Data (수치형 데이터의 정규화)
16-1.Z-score(Z 점수, 표준 점수) : 각 raw data가 표준편차 상에서 어떤 위치에 있는지를 나타냄

(x = 정규화할 값, μ = 모집단 평균, σ = 표준 편차)
- data가 평균보다 작다면 음수, 평균보다 크다면 양수의 값을 가짐
16-2. Mean Absolute Deviation (평균 절대 편차)
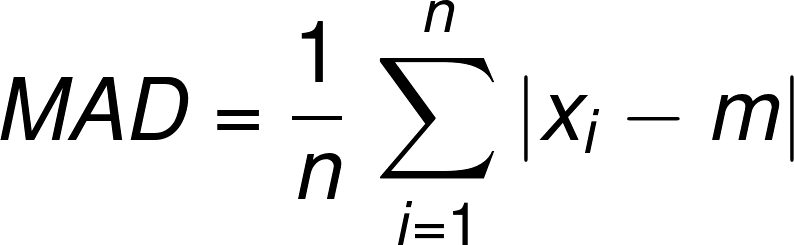
(n = data object의 개수, m = 평균)
- 평균 절대 편차를 Z-score에 표준편차 대신 사용하는 것이 더 성능이 뛰어남

17. Distance on Numeric Data : Minkowski Distance (민코브스키 거리)
- x = ( x1, x2, x3, ..., xn)과 y = (y1, y2, y3, ... , yn)이 n개의 attribute를 가진 data object일때

(p는 1보다 큰 실수로, 거리의 차수. 차수가 p인 거리는 L-p norm)
- 특징
- positive definiteness : i ≠ j라면, d(i, j) > 0 이고, d(i, i)는 0
- Symmetry : d(i, j) == d(j, i)
- Triangle inequality : d(i, j) ≤ d(i, k) + d(k, j)
17-1. 민코브스키 거리의 유형
- p = 1 : Manhattan Distance (city block distance, L-1 norm distance), 맨하탄 거리

- p = 2 : Euclidean Distance (L-2 norm distance), 유클리드 거리

- p ->∞ : Supremum Distance ( L-max norm distance, L-∞ norm distance), 최소 상계 거리
- 2개의 data objects의 attribute중 값의 최대 차이를 보이는 attribute로 계산
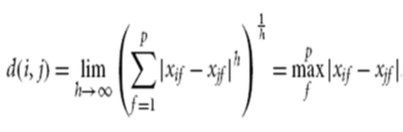
18. Cosine Similarity (코사인 유사도)
: 두 vector 사이의 유사도를 측정

- A·B = vector의 dot product (점곱), ||A|| ||B|| = vector 의 길이